RS Aggarwal Class 9 Chapter Lines & Angles Exercise 4C Solution

EXERCISE 4C

Question 1:
Since AB and CD are given to be parallel lines and t is a transversal.
So, ∠5 = ∠1 = 70^o [Corresponding angles are equal]
∠3 = ∠1 = 70^o [Vertically opp. Angles]
∠3 + ∠6 = 180^o [Co-interior angles on same side]
∴ ∠6 = 180^o – ∠3
= 180^o – 70^o = 110^o
∠6 = ∠8 [Vertically opp. Angles]
⇒ ∠8 = 110^o
⇒ ∠4 + ∠5 = 180^o [Co-interior angles on same side]
∠4 = 180^o – 70^o = 110^o
∠2 = ∠4 = 110^o [ Vertically opposite angles]
∠5 = ∠7 [Vertically opposite angles]
So, ∠7 = 70^o
∴ ∠2 = 110^o, ∠3 = 70^o , ∠4 = 110^o, ∠5 = 70^o, ∠6 = 110^o, ∠7 = 70^o and ∠8 = 110^o.

Question 2:
Since ∠2 : ∠1 = 5 : 4.
Let ∠2 and ∠1 be 5x and 4x respectively.
Now, ∠2 + ∠1 = 180^o , because ∠2 and ∠1 form a linear pair.
So, 5x + 4x = 180^o
⇒ 9x = 180^o
⇒ x = 20^o
∴ ∠1 = 4x = 4 × 20^o = 80^o
And ∠2 = 5x = 5 × 20^o = 100^o
∠3 = ∠1 = 80^o [Vertically opposite angles]
And ∠4 = ∠2 = 100^o [Vertically opposite angles]
∠1 = ∠5 and ∠2 = ∠6 [Corresponding angles]
So, ∠5 = 80^o and ∠6 = 100^o
∠8 = ∠6 = 100^o [Vertically opposite angles]
And ∠7 = ∠5 = 80^o [Vertically opposite angles]
Thus, ∠1 = 80^o, ∠2 = 100^o, ∠3 = ∠80^o, ∠4 = 100^o, ∠5 = 80^o, ∠6 = 100^o, ∠7 = 80^o and ∠8 = 100^o.

Question 3:
Given: AB || CD and AD || BC
To Prove: ∠ADC = ∠ABC
Proof: Since AB || CD and AD is a transversal. So sum of consecutive interior angles is 180^o.
⇒ ∠BAD + ∠ADC = 180^o ….(i)
Also, AD || BC and AB is transversal.
So, ∠BAD + ∠ABC = 180^o ….(ii)
From (i) and (ii) we get:
∠BAD + ∠ADC = ∠BAD + ∠ABC
⇒ ∠ADC = ∠ABC (Proved)

Question 4:
(i) Through E draw EG || CD. Now since EG||CD and ED is a transversal.

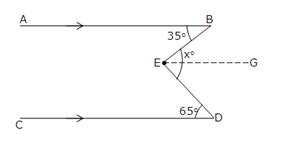
So, ∠GED = ∠EDC = 65^o [Alternate interior angles]
Since EG || CD and AB || CD,
EG||AB and EB is transversal.
So, ∠BEG = ∠ABE = 35^o [Alternate interior angles]
So, ∠DEB = x^o
⇒ ∠BEG + ∠GED = 35^o + 65^o = 100^o.
Hence, x = 100.
(ii) Through O draw OF||CD.

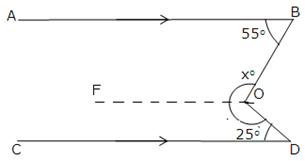
Now since OF || CD and OD is transversal.
∠CDO + ∠FOD = 180^o
[sum of consecutive interior angles is 180^o]
⇒ 25^o + ∠FOD = 180^o
⇒ ∠FOD = 180^o – 25^o = 155^o
As OF || CD and AB || CD [Given]
Thus, OF || AB and OB is a transversal.
So, ∠ABO + ∠FOB = 180^o [sum of consecutive interior angles is 180^o]
⇒ 55^o + ∠FOB = 180^o
⇒ ∠FOB = 180^o – 55^o = 125^o
Now, x^o = ∠FOB + ∠FOD = 125^o + 155^o = 280^o.
Hence, x = 280.
(iii) Through E, draw EF || CD.

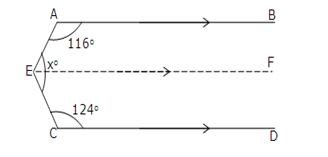
Now since EF || CD and EC is transversal.
∠FEC + ∠ECD = 180^o
[sum of consecutive interior angles is 180^o]
⇒ ∠FEC + 124^o = 180^o
⇒ ∠FEC = 180^o – 124^o = 56^o
Since EF || CD and AB ||CD
So, EF || AB and AE is a trasveral.
So, ∠BAE + ∠FEA = 180^o
[sum of consecutive interior angles is 180^o]
∴ 116^o + ∠FEA = 180^o
⇒ ∠FEA = 180^o – 116^o = 64^o
Thus, x^o = ∠FEA + ∠FEC
= 64^o + 56^o = 120^o.
Hence, x = 120.

Question 5:
Since AB || CD and BC is a transversal.
So, ∠ABC = ∠BCD [atternate interior angles]
⇒ 70^o = x^o + ∠ECD ….(i)
Now, CD || EF and CE is transversal.
So, ∠ECD + ∠CEF = 180^o [sum of consecutive interior angles is 180^o]
∴ ∠ECD + 130^o = 180^o
⇒ ∠ECD = 180^o – 130^o = 50^o
Putting ∠ECD = 50^o in (i) we get,
70^o = x^o + 50^o
⇒ x = 70 – 50 = 20

Question 6:
Through C draw FG || AE

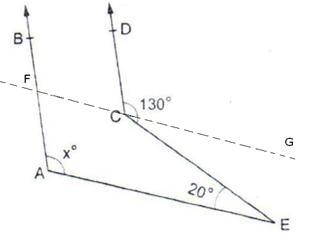
Now, since CG || BE and CE is a transversal.
So, ∠GCE = ∠CEA = 20^o [Alternate angles]
∴ ∠DCG = 130^o – ∠GCE
= 130^o – 20^o = 110^o
Also, we have AB || CD and FG is a transversal.
So, ∠BFC = ∠DCG = 110^o [Corresponding angles]
As, FG || AE, AF is a transversal.
∠BFG = ∠FAE [Corresponding angles]
∴ x^o = ∠FAE = 110^o.
Hence, x = 110

Question 7:
Given: AB || CD
To Prove: ∠BAE – ∠DCE = ∠AEC

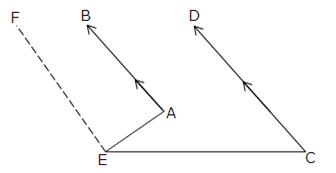
Construction : Through E draw EF || AB
Proof : Since EF || AB, AE is a transversal.
So, ∠BAE + ∠AEF = 180^O ….(i)
[sum of consecutive interior angles is 180^o]
As EF || AB and AB || CD [Given]
So, EF || CD and EC is a transversal.
So, ∠FEC + ∠DCE = 180^o ….(ii)
[sum of consecutive interior angles is 180^o]
From (i) and (ii) we get,
∠BAE + ∠AEF = ∠FEC + ∠DCE
⇒ ∠BAE – ∠DCE = ∠FEC – ∠AEF = ∠AEC [Proved]

Question 8:
Since AB || CD and BC is a transversal.
So, ∠BCD = ∠ABC = x^o [Alternate angles]
As BC || ED and CD is a transversal.
∠BCD + ∠EDC = 180^o
⇒ ∠BCD + 75^o =180^o
⇒ ∠BCD = 180^o – 75^o = 105^o
∠ABC = 105^o [since ∠BCD = ∠ABC]
∴ x^o = ∠ABC = 105^o
Hence, x = 105.

Question 9:
Through F, draw KH || AB || CD

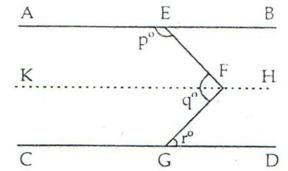
Now, KF || CD and FG is a transversal.
⇒ ∠KFG = ∠FGD = r^o …. (i)
[alternate angles]
Again AE || KF, and EF is a transversal.
So, ∠AEF + ∠KFE = 180^o
∠KFE = 180^o – p^o …. (ii)
Adding (i) and (ii) we get,
∠KFG + ∠KFE = 180 – p + r
⇒ ∠EFG = 180 – p + r
⇒ q = 180 – p + r
i.e., p + q – r = 180

Question 10:

Since AB || PQ and EF is a transversal.
So, ∠CEB = ∠EFQ [Corresponding angles]
⇒ ∠EFQ = 75^o
⇒ ∠EFG + ∠GFQ = 75^o
⇒ 25^o + y^o = 75^o
⇒ y = 75 – 25 = 50
Also, ∠BEF + ∠EFQ = 180^o [sum of consecutive interior angles is 180^o]
∠BEF = 180^o – ∠EFQ
= 180^o – 75^o
∠BEF = 105^o
∴ ∠FEG + ∠GEB = ∠BEF = 105^o
⇒ ∠FEG = 105^o – ∠GEB = 105^o – 20^o = 85^o
In ∆EFG we have,
x^o + 25^o + ∠FEG = 180^o

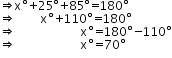
Hence, x = 70.

Question 11:
Since AB || CD and AC is a transversal.
So, ∠BAC + ∠ACD = 180^o [sum of consecutive interior angles is 180^o]
⇒ ∠ACD = 180^o – ∠BAC
= 180^o – 75^o = 105^o
⇒ ∠ECF = ∠ACD [Vertically opposite angles]
∠ECF = 105^o
Now in ∆CEF,
∠ECF + ∠CEF + ∠EFC =180^o
⇒ 105^o + x^o + 30^o = 180^o
⇒ x = 180 – 30 – 105 = 45
_{Hence, x = 45.}

Question 12:
Since AB || CD and PQ a transversal.
So, ∠PEF = ∠EGH [Corresponding angles]
⇒ ∠EGH = 85^o
∠EGH and ∠QGH form a linear pair.
So, ∠EGH + ∠QGH = 180^o
⇒ ∠QGH = 180^o – 85^o = 95^o
Similarly, ∠GHQ + 115^o = 180^o
⇒ ∠GHQ = 180^o – 115^o = 65^o
In ∆GHQ, we have,
x^o + 65^o + 95^o = 180^o
⇒ x = 180 – 65 – 95 = 180 – 160
∴ x = 20

Question 13:

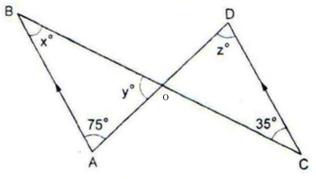
Since AB || CD and BC is a transversal.
So, ∠ABC = ∠BCD
⇒ x = 35
Also, AB || CD and AD is a transversal.
So, ∠BAD = ∠ADC
⇒ z = 75
In ∆ABO, we have,
∠AOB + ∠BAO + ∠BOA = 180^o
⇒ x^o + 75^o + y^o = 180^o
⇒ 35 + 75 + y = 180
⇒ y = 180 – 110 = 70
∴ x = 35, y = 70 and z = 75.

Question 14:

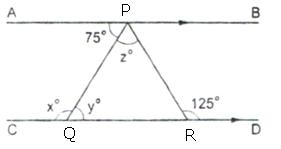
Since AB || CD and PQ is a transversal.
So, y = 75 [Alternate angle]
Since PQ is a transversal and AB || CD, so x + APQ = 180^o
[Sum of consecutive interior angles]
⇒ x^o = 180^o – APQ
⇒ x = 180 – 75 = 105
Also, AB || CD and PR is a transversal.
So, ∠APR = ∠PRD [Alternate angle]
⇒ ∠APQ + ∠QPR = ∠PRD [Since ∠APR = ∠APQ + ∠QPR]
⇒ 75^o + z^o = 125^o
⇒ z = 125 – 75 = 50
∴ x = 105, y = 75 and z = 50.

Question 15:
∠PRQ = x^o = 60^o [vertically opposite angles]
Since EF || GH, and RQ is a transversal.
So, ∠x = ∠y [Alternate angles]
⇒ y = 60
AB || CD and PR is a transversal.
So, ∠PRD = ∠APR [Alternate angles]
⇒ ∠PRQ + ∠QRD = ∠APR [since ∠PRD = ∠PRQ + ∠QRD]
⇒ x + ∠QRD = 110^o
⇒ ∠QRD = 110^o – 60^o = 50^o
In ∆QRS, we have,
∠QRD + t^o + y^o = 180^o
⇒ 50 + t + 60 = 180
⇒ t = 180 – 110 = 70
Since, AB || CD and GH is a transversal
So, z^o = t^o = 70^o [Alternate angles]
∴ x = 60 , y = 60, z = 70 and t = 70

Question 16:
(i) Lines l and m will be parallel if 3x – 20 = 2x + 10
[Since, if corresponding angles are equal, lines are parallel]
⇒ 3x – 2x = 10 + 20
⇒ x = 30
(ii) Lines will be parallel if (3x + 5)^o + 4x^o = 180^o
[if sum of pairs of consecutive interior angles is 180^o, the lines are parallel]
So, (3x + 5) + 4x = 180
⇒ 3x + 5 + 4x = 180
⇒ 7x = 180 – 5 = 175
⇒ x = \(\frac { 175 }{ 7 } \) = 25

Question 17:
Given: Two lines m and n are perpendicular to a given line l.

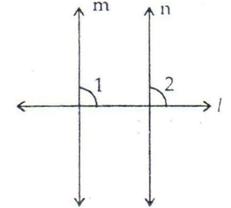
To Prove: m || n
Proof : Since m ⊥ l
So, ∠1 = 90^o
Again, since n ⊥ l
∠2 = 90^o
∴ ∠1 = ∠2 = 90^o
But ∠1 and ∠2 are the corresponding angles made by the transversal l with lines m and n and they are proved to be equal.
Thus, m || n.