RS Aggarwal Class 9 Math Chapter 2 Polynomials Exercise 2K Solution
EXERCISE 2K
Question 1:
125a3 + b3 + 64c3 – 60abc
= (5a)3 + (b)3 + (4c)3 – 3 (5a) (b)
(4c)
= (5a + b + 4c) [(5a)2 + b2 + (4c)2 – (5a)
(b) – (b) (4c) – (5a) (4c)]
[∵ a3 + b3 + c3 – 3abc = (a+ b + c)
(a2 + b2 + c2 – ab – bc –
ca)]
= (5a + b + 4c) (25a2 + b2 + 16c2 – 5ab
– 4bc – 20ac).
Question 2:
a3 + 8b3 + 64c3 – 24abc
= (a)3 + (2b)3 + (4c)3 – 3 a 2b 4c
= (a + 2b + 4c) [a2 + 4b2 + 16c2 – 2ab
– 8bc – 4ca).
Question 3:
1 + b3 + 8c3 – 6bc
= 1 + (b)3 + (2c)3 – 3 (b) (2c)
= (1 + b + 2c) [1 + b2 + (2c)2 – b – b 2c –
2c]
= (1 + b + 2c) (1 + b2 + 4c2 – b – 2bc –
2c).
Question 4:
216 + 27b3 + 8c3 – 108bc
= (6)3 + (3b)3 + (2c)2 – 3 6 3b 2c
= (6 + 3b + 2c) [(6)2 + (3b)2 + (2c)2 – 6 3b
– 3b 2c – 2c 6]
= (6 + 3b + 2c) (36 + 9b2 + 4c2 – 18b – 6bc
– 12c).
Question 5:
27a3 – b3 + 8c3 + 18abc
= (3a)3 + (-b)3 + (2c)3 + 3(3a) (-b) (2c)
= [3a + (-b) + 2c] [(3a)2 + (-b)2 + (2c)2 –
3a (-b) – (-b) (2c) – (2c) (3a)]
= (3a – b + 2c) (9a2 + b2 + 4c2 + 3ab + 2bc
– 6ca).
Question 6:
8a3 + 125b3 – 64c3 + 120abc
= (2a)3 + (5b)3 + (-4c)3 – 3 (2a) (5b)
(-4c)
= (2a + 5b – 4c) [(2a)2 + (5b)2 + (-4c)2
– (2a) (5b) – (5b) (-4c) – (-4c) (2a)]
= (2a + 5b – 4c) (4a2 + 25b2 + 16c2 –
10ab + 20bc + 8ca).
Question 7:
8 – 27b3 – 343c3 – 126bc
= (2)3 + (-3b)3 + (-7c)3 – 3(2) (-3b)
(-7c)
= (2 – 3b – 7c) [(2)2 + (-3b)2 + (-7c)2
– (2) (-3b) – (-3b) (-7c) – (-7c) (2)]
= (2 – 3b – 7c) (4 + 9b2 + 49c2 + 6b – 21bc
+ 14c).
Question 8:
125 – 8x3 – 27y3 – 90xy
= (5)3 + (-2x)3 + (-3y)3 – 3 (5) (-2x)
(-3y)
= (5 – 2x – 3y) [(5)2 + (-2x)2 + (-3y)2
– (5) (-2x) – (-2x) (-3y) – (-3y) (5)]
= (5 – 2x – 3y) (25 + 4x2 + 9y2 + 10x – 6xy
+ 15y).
Question 9:
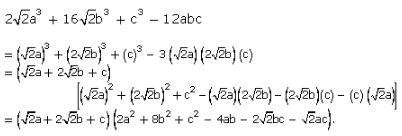
Question 10:
x3 + y3 – 12xy + 64
= x3 + y3 + 64 – 12xy
= (x)3 + (y)3 + (4)3 – 3 (x) (y) (4)
= (x + y + 4) [(x)2 + (y)2 + (4)2 – x × y
– y × 4 – 4 × x ]
= (x + y + 4) (x2 + y2 + 16 – xy – 4y – 4x).
Question 11:
Putting (a – b) = x, (b – c) = y and (c – a) = z, we get,
(a – b)3 + (b – c)3 + (c –
a)3
= x3 + y3 + z3, where (x + y + z) = (a – b) +
(b – c) + (c – a) = 0
= 3xyz [∵ (x + y + z) = 0 ⇒ (x3 + y3 + z3) =
3xyz]
= 3(a – b) (b – c) (c – a).
Question 12:
We have:
(3a – 2b) + (2b – 5c) + (5c – 3a) = 0
So, (3a – 2b)3 + (2b – 5c)3 + (5c –
3a)3
= 3(3a – 2b) (2b – 5c) (5c – 3a).
Question 13:
a3 (b – c)3 + b3 (c – a)3 +
c3 (a – b)3
= [a (b – c)]3 + [b (c – a)]3 + [c (a –
b)]3
Now, since, a (b – c) + b (c -a) + c (a – b)
= ab – ac + bc – ba + ca – bc = 0
So, a3 (b – c)3 + b3 (c –
a)3 + c3 (a – b)3
= 3a (b – c) b (c – a) c (a – b)
= 3abc (a – b) (b – c) (c – a).
Question 14:
(5a – 7b)3 + (9c – 5a)3 + (7b –
9c)3
Since, (5a – 7b) + (9c – 5a) + (7b – 9c)
= 5a – 7b + 9c – 5a + 7b – 9c = 0
So, (5a – 7b)3 + (9c – 5a)3 + (7b –
9c)3
= 3(5a – 7b) (9c – 5a) (7b – 9c).
Question 15:
(x + y – z) (x2 + y2 + z2 – xy + yz +
zx)
= [x + y + (-z)] [(x)2 + (y)2 + (-z)2 – (x)
(y) – (y) (-z) – (-z) (x)]
= x3 + y3 – z3 + 3xyz.
Question 16:
(x – 2y + 3) (x2 + 4y2 + 2xy – 3x + 6y + 9)
= [x + (-2y) + 3] [(x)2 + (-2y)2 + (3) – (x) (-2y)
– (-2y) (3) – (3) (x)]
= (a + b + c) (a2 + b2 + c2 – ab – bc
– ca)
= a3 + b3 + c3 – 3abc
Where, x = a, (-2y) = b and 3 = c
(x – 2y + 3) (x2 + 4y2 + 2xy – 3x + 6y + 9)
= (x)3 + (-2y)3 + (3)2 – 3 (x) (-2y)
(3)
= x3 – 8y3 + 27 + 18xy.
Question 17:
(x – 2y – z) (x2 + 4y2 + z2 + 2xy + zx
– 2yz)
= [x + (-2y) + (-z)] [(x)2 + (-2y)2 + (-z)2 –
(x) (-2y) – (-2y) (-z) – (-z) (x)]
= (a + b + c) (a2 + b2 + c2 – ab – bc
– ca)
= a3 + b3 + c3 – 3abc
Where x = a, (-2y) = b and (-z) = c
(x – 2y – z) (x2 + 4y2 + z2 + 2xy + zx
– 2yz)
= (x)3 + (-2y)3 + (-z)3 – 3 (x) (-2y)
(-z)
= x3 – 8y3 – z3 – 6xyz.
Question 18:
Given, x + y + 4 = 0
We have (x3 + y3 – 12xy + 64)
= (x)3 + (y)3 + (4)3 – 3 (x) (y) (4)
= 0.
Since, we know a + b + c = 0 ⇒ (a3 + b3 + c3) =
3abc
Question 19:
Given x = 2y + 6
Or, x ̵#8211; 2y – 6 = 0
We have, (x3 – 8y3 – 36xy – 216)
= (x3 – 8y3 – 216 – 36xy)
= (x)3 + (-2y)3 + (-6)3 – 3 (x) (-2y)
(-6)
= (x – 2y – 6) [(x)2 + (-2y)2 + (-6)2
– (x) (-2y) – (-2y) (-6) – (-6) (x)]
= (x – 2y – 6) (x2 + 4y2 + 36 + 2xy – 12y +
6x)
= 0 (x2 + 4y2 + 36 + 2xy – 12y + 6x)
= 0.