RS Aggarwal Solutions Class 9 Chapter 14 Statistics Solution

EXERCISE 14F

Question 1:
For calculating the mean , we prepare the following table :

Daily wages (in Rs ) (Xi)	No of workers (fi)	fixi
90 110 120 130 150	12 14 13 11 10	1080 1540 1560 1430 1500
	\(\sum { { f }_{ i } } =60 \)	7110

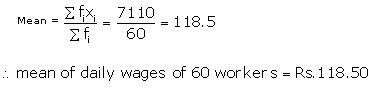
Question 2:
For calculating the mean , we prepare the following frequency table :

Weight (in kg) (Xi)	No of workers (fi)	fiXi
60 63 66 69 72	4 3 2 2 1	240 189 132 138 72
	\(\sum { { f }_{ i } } =12 \)	771

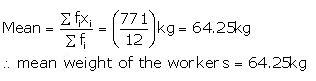
Question 3:
For calculating the mean , we prepare the following frequency table :

Age (in years) (Xi)	Frequency (fi)	fiXi
15 16 17 18 19 20	3 8 9 11 6 3	45 128 153 198 114 60
	\(\sum { { f }_{ i } } =40 \)	698

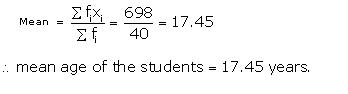
Question 4:
For calculating the mean , we prepare the following frequency table :

Variable (Xi)	Frequency (fi)	fiXi
10 30 50 70 89	7 8 10 15 10	70 240 500 1050 890
	\(\sum { { f }_{ i } } =50 \)	\(\sum { { f }_{ i } } { x }_{ i }=2750 \)

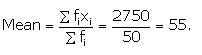
Question 5:
We prepare the following frequency table :

(Xi)	(fi)	fiXi
3 5 7 9 11 13	6 8 15 P 8 4	18 40 105 9P 88 52
	\(\sum { { f }_{ i } } =41+p \)	\(\sum { { f }_{ i } } { x }_{ i }=303+9p \)

⇒ 303 + 9p = 8(41+p)
⇒ 303 + 9p= 328 + 8p
⇒ 9p – 8p = 328 -303
⇒ P=25
∴ the value of P=25

Question 6:
We prepare the following frequency distribution table:

(Xi)	(fi)	fiXi
15 20 25 30 35 40	8 7 P 14 15 6	120 140 25p 420 525 240
	\(\sum { { f }_{ i } } =50+p \)	\(\sum { { f }_{ i } } { x }_{ i }=1445+25p \)

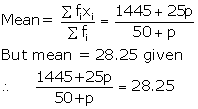
⇒ 1445 + 25p = (28.25)(50+p)
⇒ 1445 + 25p = 1412.50 + 28.25p
⇒ -28.25p + 25p = -1445 + 1412.50
⇒ -3.25p = -32.5
⇒ \(\frac { 32.5 }{ 3.25 } \) = 10
∴ the value of p=10

Question 7:
We prepare the following frequency distribution table:

(Xi)	(fi)	fiXi
8 12 15 P 20 25 30	12 16 20 24 16 8 4	96 192 300 24p 320 200 120
	\(\sum { { f }_{ i } } =100 \)	\(\sum { { f }_{ i } } { x }_{ i }=1228+24p \)

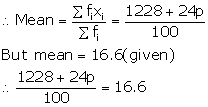
⇒ 1228 + 24p = 1660
⇒ 24p = 1660-1228
⇒ 24p = 432
⇒ \(\frac { 432 }{ 24 } \) = 18
∴ the value of p =18

Question 8:
Let f₁ and f₂ be the missing frequencies.
We prepare the following frequency distribution table.

(Xi)	(fi)	fixi
10 30 50 70 90	17 f1 32 f2 19	170 30f1 1600 70f2 1710
Total	120	3480 + 30f1 + 70f2

Here,

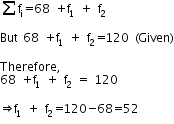
Thus, f₂ = 52 – f₁…….(1)
Also,

Substituting the value of f1 in equation 1, we have,
f2=52 – 28 = 24
Thus, the missing frequencies are f1 =28 and f2=24 respectively.

Question 9:
Let the assumed mean (A) =900

Weekly wages (Xi)	No of workers (fi)	di=(xi-A) =xi-900	fi x di
800 820 860 900 920 980 1000	7 14 19 25 20 10 5	-100 -80 -40 0 20 80 100	-700 -1120 -760 0 400 800 500
	\(\sum { { f }_{ i } } =100 \)		-880

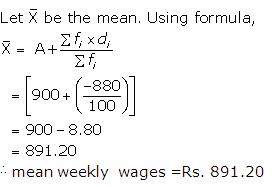
Question 10:
Let the assumed mean be A = 67

Height in cm (Xi)	No of plants (fi)	di=(xi-A) =(xi-67)	fi di
61 64 67 70 73	5 18 42 27 8	-6 -3 0 3 6	-30 -54 0 81` 48
		100	\(\sum { { f }_{ i } } { d }_{ i }=45 \)

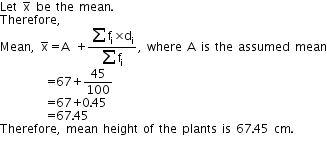
Question 11:
Clearly, h=1. Let the assumed mean A=21

(Xi)	(fi)	\({ u }_{ i }=\frac { { x }_{ i }-21 }{ 1 } \)	fiui
18 19 20 21 22 23 24	170 320 530 700 230 140 110	-3 -2 -1 0 1 2 3	-510 -640 -530 0 230 280 330
Total	\(\sum { { f }_{ i } } =2200 \)		\(\sum { { f }_{ i } } { u }_{ i }=-840 \)

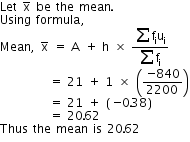
Question 12:
Clearly, h= (x2- x1)
=(600-200)=400
Let assumed mean A =1000

Height (in m) (Xi)	No of villages (fi)	\({ u }_{ i }=\frac { { x }_{ i }-1000 }{ 400 } \)	fixui
200 600 1000 1400 1800 2200	142 265 560 271 89 16	-2 -1 0 1 2 3	-284 -265 0 271 178 48
Total	\(\sum { { f }_{ i } } =1343 \)		\(\sum { { f }_{ i } } { u }_{ i }=-52 \)