RS Aggarwal Class 9 Math Chapter 2 Polynomials Exercise 2C Solution

EXERCISE 2C

Question 1:
f(x) = x³ – 6x² + 9x + 3
Now, x – 1 = 0 ⇒ x = 1
By the remainder theorem, we know that when f(x) is divided by (x – 1) the remainder is f(1).
Now, f(1) = 1³ – 6 × 1² + 9 × 1 + 3
= 1 – 6 + 9 + 3
= 13 – 6 = 7
∴ The required remainder is 7.

Question 2:
f(x) = (2x³ – 5x² + 9x – 8)
Now, x – 3 = 0 ⇒ x = 3
By the remainder theorem, we know that when f(x) is divided by (x – 3) the remainder is f(3).
Now, f(3) = 2 × 3³ – 5 × 3² + 9 × 3 – 8
= 54 – 45 + 27 – 8
= 81 – 53 = 28
∴ The required remainder is 28.

Question 3:
f(x) = (3x⁴ – 6x² – 8x + 2)
Now, x – 2 = 0 ⇒ x = 2
By the remainder theorem, we know that when f(x) is divided by (x – 2) the remainder is f(2).
Now, f(2) = 3 × 2⁴ – 6 × 2² – 8 × 2 + 2
= 48 – 24 – 16 + 2
= 50 – 40 = 10
∴ The required remainder is 10.

Question 4:
f(x) = x³ – 7x² + 6x + 4
Now, x – 6 = 0 ⇒ x = 6
By the remainder theorem, we know that when f(x) is divide by (x – 6) the remainder is f(6)
Now, f(6) = 6³ – 7 × 6² + 6 × 6 + 4
= 216 – 252 + 36 + 4
= 256 – 252 = 4
∴ The required remainder is 4.

Question 5:
f(x) = (x³ – 6x² + 13x + 60)
Now, x + 2 = 0 ⇒ x = -2
By the remainder the theorem, we know that when f(x) is divide by (x + 2) the remainder is f(-2).
Now, f(-2) = (-2)³ – 6(-2)² + 13(-2) + 60
= -8 – 24 – 26 + 60
= -58 + 60 = 2
∴ The required remainder is 2.

Question 6:
f(x) = (2x⁴ + 6x³ + 2x² + x – 8)
Now, x + 3 = 0 ⇒ x = -3
By the remainder the theorem, we know that when f(x) is divide by (x + 3) the remainder is f(-3).
f(-3) = 2(-3)⁴ + 6(-3)³ + 2(-3)² – 3 – 8
= 162 – 162 + 18 – 3 – 8
= 18 – 11 = 7
∴ The required remainder is 7.

Question 7:
f(x) = (4x³ – 12x² + 11x – 5)
Now, 2x – 1 = 0 ⇒ x = \(\frac { 1 }{ 2 } \)
By the remainder theorem, we know that when f(x) is divided by (2x – 1) the remainder is \(f\left( \frac { 1 }{ 2 } \right) \)

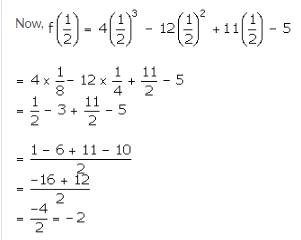
∴ The required remainder is -2.

Question 8:
f(x) = (81x⁴ + 54x³ – 9x² – 3x + 2)
Now, 3x + 2 = 0 ⇒ x = \(\frac { -2 }{ 3 } \)
By the remainder theorem, we know that when f(x) is divided by (3x+ 2) the remainder is \(f\left( \frac { -2 }{ 3 } \right) \)

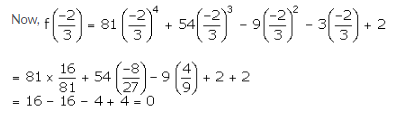
∴ The required remainder is 0.

Question 9:
f(x) = (x³ – ax² + 2x – a)
Now, x – a = 0 x ⇒ = a
By the remainder theorem, we know that when f(x) is divided by (x – a) the remainder is f(a)
Now, f(a) = a³ – a a² + 2 a – a
= a³ – a³ + 2a – a
= a
∴ The required remainder is a.

Question 10:
Let f(x) = ax³ + 3x² – 3
and g(x) = 2x³ – 5x + a
∴ f(4) = a × 4³ + 3 × 4² – 3
= 64a + 48 – 3
= 64a + 45
g(4) = 2 × 4³ – 5 × 4 + a
= 128 – 20 + a
= 108 + a
_{It is given that:}
f(4) = g(4)
⇒ 64a + 45 = 108 + a
⇒ 64a – a = 108 – 45
⇒ 63a = 63
⇒ a = \(\frac { 63 }{ 63 } \) = 1
∴ The value of a is 1.

Question 11:
Let f(x) = (x⁴ – 2x³ + 3x² – ax + b)
∴ From the given information,
f(1) = 1⁴ – 2(1)³ + 3(1)² – a (1 ) + b = 5
⇒ 1 – 2 + 3 – a + b = 5
⇒ 2 – a + b = 5 ….(i)
And,
f(-1) = (-1)⁴ – 2(-1)³ + 3(-1)² – a(-1) + b = 19
⇒ 1 + 2 + 3 + a + b = 19
⇒ 6 + a + b = 19 ….(ii)
Adding (i) and (ii), we get
⇒ 8 + 2b = 24
⇒ 2b = 24 – 8 = 16
⇒ b = \(\frac { 16 }{ 2 } \)
Substituting the value of b = 8 in (i), we get
2 – a + 8 = 5
⇒ -a + 10 = 5
⇒ -a = -10 + 5
⇒ -a = -5
⇒ a = 5
∴ a = 5 and b = 8
f(x) = x⁴ – 2x³ + 3x² – ax + b
= x⁴ – 2x³ + 3x² – 5x + 8
∴ f(2) = (2)⁴ – 2(2)³ + 3(2)² – 5(2) + 8
= 16 – 16 + 12 – 10 + 8
= 20 – 10 = 10
∴ The required remainder is 10.