RS Aggarwal Class 9 Chapter Lines & Angles Exercise 4A Solution

EXERCISE 4A

Question 1:
(i) Angle: Two rays having a common end point form an angle.
(ii) Interior of an angle: The interior of ∠AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
(iii) Obtuse angle: An angle whose measure is more than 90° but less than 180°, is called an obtuse angle.
(iv) Reflex angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle.
(v) Complementary angles: Two angles are said to be complementary, if the sum of their measures is 90o.
(vi) Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°.

Question 2:
∠A = 36° 27′ 46″ and ∠B = 28° 43′ 39″
∴ Their sum = (36° 27′ 46″) + (28° 43′ 39″)

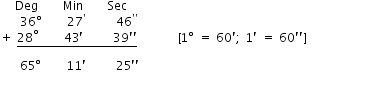
Therefore, the sum ∠A + ∠B = 65° 11′ 25″

Question 3:
Let ∠A = 36° and ∠B = 24° 28′ 30″
Their difference = 36° – 24° 28′ 30″

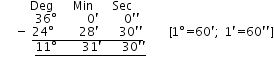
Thus the difference between two angles is ∠A – ∠B = 11° 31′ 30″

Question 4:
(i) Complement of 58^o = 90^o – 58^o = 32^o
(ii) Complement of 16^o = 90 – 16^o = 74^o
(iii) \(\frac { 2 }{ 3 } \) of a right angle = \(\frac { 2 }{ 3 } \) × 90^o = 60^o
Complement of 60^o = 90^o – 60^o = 30^o
(iv) 1^o = 60′
⇒ 90^o = 89^o 60′

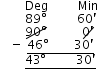
Complement of 46^o 30′ = 90^o – 46^o 30′ = 43^o 30′
(v) 90^o = 89^o 59′ 60″

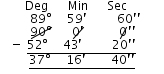
Complement of 52^o 43′ 20″ = 90^o – 52^o 43′ 20″
= 37^o 16′ 40″
(vi) 90^o = 89^o 59′ 60″

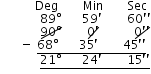
∴ Complement of (68^o 35′ 45″)
= 90^o – (68^o 35′ 45″)
= 89^o 59′ 60″ – (68^o 35′ 45″)
= 21^o 24′ 15″

Question 5:
(i) Supplement of 63^o = 180^o – 63^o = 117^o
(ii) Supplement of 138^o = 180^o – 138^o = 42^o
(iii) \(\frac { 3 }{ 5 } \) of a right angle = \(\frac { 3 }{5 } \) × 90^o = 54^o
∴ Supplement of 54^o = 180^o – 54^o = 126^o
(iv) 1^o = 60′
⇒ 180^o = 179^o 60′

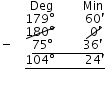
Supplement of 75^o 36′ = 180^o – 75^o 36′ = 104^o 24′
(v) 1^o = 60′, 1′ = 60″
⇒ 180^o = 179^o 59′ 60″

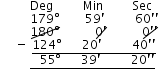
Supplement of 124^o 20′ 40″ = 180^o – 124^o 20′ 40″
= 55^o 39′ 20″
(vi) 1^o = 60′, 1′ = 60″
⇒ 180^o = 179^o 59′ 60″

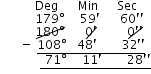
∴ Supplement of 108^o 48′ 32″ = 180^o – 108^o 48′ 32″
= 71^o 11′ 28″.

Question 6:
(i) Let the required angle be x^o
Then, its complement = 90^o – x^o

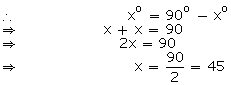
∴ The measure of an angle which is equal to its complement is 45^o.
(ii) Let the required angle be x^o
Then, its supplement = 180^o – x^o

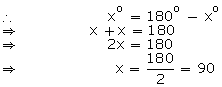
∴ The measure of an angle which is equal to its supplement is 90^o.

Question 7:
Let the required angle be x^o
Then its complement is 90^o – x^o

∴ The measure of an angle which is 36^o more than its complement is 63^o.

Question 8:
Let the required angle be x^o
Then its supplement is 180^o – x^o

∴ The measure of an angle which is 25^o less than its supplement is

Question 9:
Let the required angle be x^o
Then, its complement = 90^o – x^o

∴ The required angle is 72^o.

Question 10:
Let the required angle be x^o
Then, its supplement is 180^o – x^o

∴ The required angle is 150^o.

Question 11:
Let the required angle be x^o
Then, its complement is 90^o – x^o and its supplement is 180^o – x^o
That is we have,

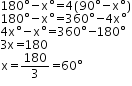
∴ The required angle is 60^o.

Question 12:
Let the required angle be x^o
Then, its complement is 90^o – x^o and its supplement is 180^o – x^o

∴ The required angle is 45^o.

Question 13:
Let the two required angles be x^o and 180^o – x^o.
Then,

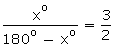
⇒ 2x = 3(180 – x)
⇒ 2x = 540 – 3x
⇒ 3x + 2x = 540
⇒ 5x = 540
⇒ x = 108
Thus, the required angles are 108^o and 180^o – x^o = 180 ^o – 108^o = 72^o.

Question 14:
Let the two required angles be x^o and 90^o – x^o.
Then

⇒ 5x = 4(90 – x)
⇒ 5x = 360 – 4x
⇒ 5x + 4x = 360
⇒ 9x = 360
⇒ x = \(\frac { 360 }{ 9 } \) = 40
Thus, the required angles are 40^o and 90^o – x^o = 90 ^o – 40^o = 50^o.

Question 15:
Let the required angle be x^o.
Then, its complementary and supplementary angles are (90^o – x) and (180^o – x) respectively.
Then, 7(90^o – x) = 3 (180^o – x) – 10^o
⇒ 630^o – 7x = 540^o – 3x – 10^o
⇒ 7x – 3x = 630^o – 530^o
⇒ 4x = 100^o
⇒ x = 25^o
Thus, the required angle is 25^o.