RS Aggarwal Class 9 Chapter Lines & Angles Exercise 4B Solution

EXERCISE 4B

Question 1:

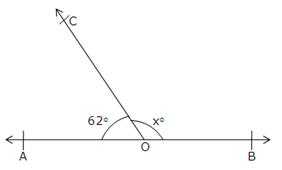
Since ∠BOC and ∠COA form a linear pair of angles, we have
∠BOC + ∠COA = 180^o
⇒ x^o + 62^o = 180^o
⇒ x = 180 – 62
∴ x = 118^o

Question 2:
Since, ∠BOD and ∠DOA form a linear pair.
∠BOD + ∠DOA = 180^o
∴ ∠BOD + ∠DOC + ∠COA = 180^o
⇒ (x + 20)^o + 55^o + (3x – 5)^o = 180^o
⇒ x + 20 + 55 + 3x – 5 = 180
⇒ 4x + 70 = 180
⇒ 4x = 180 – 70 = 110
⇒ x = \(\frac { 110 }{ 4 } \) = 27.5
∴ ∠AOC = (3 × 27.5 – 5)^o = 82.5-5 = 77.5^o
And, ∠BOD = (x + 20)^o = 27.5^o + 20^o = 47.5^o.

Question 3:
Since ∠BOD and ∠DOA from a linear pair of angles.
⇒ ∠BOD + ∠DOA = 180^o
⇒ ∠BOD + ∠DOC + ∠COA = 180^o
⇒ x^o + (2x – 19)^o + (3x + 7)^o = 180^o
⇒ 6x – 12 = 180
⇒ 6x = 180 + 12 = 192
⇒ x = \(\frac { 192 }{ 6 } \) = 32
⇒ x = 32
⇒ ∠AOC = (3x + 7)^o = (3 32 + 7)^o = 103^o
⇒ ∠COD = (2x – 19)^o = (2 32 – 19)^o = 45^o
and ∠BOD = x^o = 32^o

Question 4:
x: y: z = 5: 4: 6
The sum of their ratios = 5 + 4 + 6 = 15
But x + y + z = 180^o
[Since, XOY is a straight line]
So, if the total sum of the measures is 15, then the measure of x is 5.
If the sum of angles is 180^o, then, measure of x = \(\frac { 5 }{ 15 } \) × 180 = 60
And, if the total sum of the measures is 15, then the measure of y is 4.
If the sum of the angles is 180^o, then, measure of y = \(\frac { 4 }{ 15 } \) × 180 = 48
And ∠z = 180^o – ∠x – ∠y
= 180^o – 60^o – 48^o
= 180^o – 108^o = 72^o
∴ x = 60, y = 48 and z = 72.

Question 5:
AOB will be a straight line, if two adjacent angles form a linear pair.
∴ ∠BOC + ∠AOC = 180^o
⇒ (4x – 36)^o + (3x + 20)^o = 180^o
⇒ 4x – 36 + 3x + 20 = 180
⇒ 7x – 16 = 180^o
⇒ 7x = 180 + 16 = 196
⇒ x = \(\frac { 196 }{ 7 } \) = 28
∴ The value of x = 28.

Question 6:
Since ∠AOC and ∠AOD form a linear pair.
∴ ∠AOC + ∠AOD = 180^o
⇒ 50^o + ∠AOD = 180^o
⇒ ∠AOD = 180^o – 50^o = 130^o
∠AOD and ∠BOC are vertically opposite angles.
∠AOD = ∠BOC
⇒ ∠BOC = 130^o
∠BOD and ∠AOC are vertically opposite angles.
∴ ∠BOD = ∠AOC
⇒ ∠BOD = 50^o

Question 7:
Since ∠COE and ∠DOF are vertically opposite angles, we have,
∠COE = ∠DOF
⇒ ∠z = 50^o
Also ∠BOD and ∠COA are vertically opposite angles.
So, ∠BOD = ∠COA
⇒ ∠t = 90^o
As ∠COA and ∠AOD form a linear pair,
∠COA + ∠AOD = 180^o
⇒ ∠COA + ∠AOF + ∠FOD = 180^o [∠t = 90^o]
⇒ t + x + 50^o = 180^o
⇒ 90^o + x^o + 50^o = 180^o
⇒ x + 140 = 180
⇒ x = 180 – 140 = 40
Since ∠EOB and ∠AOF are vertically opposite angles
So, ∠EOB = ∠AOF
⇒ y = x = 40
Thus, x = 40 = y = 40, z = 50 and t = 90

Question 8:
Since ∠COE and ∠EOD form a linear pair of angles.
⇒ ∠COE + ∠EOD = 180^o
⇒ ∠COE + ∠EOA + ∠AOD = 180^o
⇒ 5x + ∠EOA + 2x = 180
⇒ 5x + ∠BOF + 2x = 180
[∴ ∠EOA and BOF are vertically opposite angles so, ∠EOA = ∠BOF]
⇒ 5x + 3x + 2x = 180
⇒ 10x = 180
⇒ x = 18
Now ∠AOD = 2x^o = 2 × 18^o = 36^o
∠COE = 5x^o = 5 × 18^o = 90^o
and, ∠EOA = ∠BOF = 3x^o = 3 × 18^o = 54^o

Question 9:
Let the two adjacent angles be 5x and 4x.
Now, since these angles form a linear pair.
So, 5x + 4x = 180^o
⇒ 9x = 180^o
⇒ x = \(\frac { 180 }{ 9 } \) = 20
∴ The required angles are 5x = 5x = 5 20^o = 100^o
and 4x = 4 × 20^o = 80^o

Question 10:
Let two straight lines AB and CD intersect at O and let ∠AOC = 90^o.

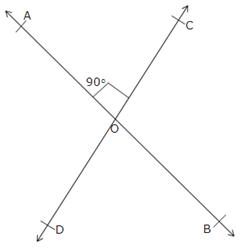
Now, ∠AOC = ∠BOD [Vertically opposite angles]
⇒ ∠BOD = 90^o
Also, as ∠AOC and ∠AOD form a linear pair.
⇒ 90^o + ∠AOD = 180^o
⇒ ∠AOD = 180^o – 90^o = 90^o
Since, ∠BOC = ∠AOD [Verticallty opposite angles]
⇒ ∠BOC = 90^o
Thus, each of the remaining angles is 90^o.

Question 11:
Since, ∠AOD and ∠BOC are vertically opposite angles.
∴ ∠AOD = ∠BOC
Now, ∠AOD + ∠BOC = 280^o [Given]
⇒ ∠AOD + ∠AOD = 280^o
⇒ 2∠AOD = 280^o
⇒ ∠AOD = \(\frac { 280 }{ 2 } \) = 140^o
⇒ ∠BOC = ∠AOD = 140^o
As, ∠AOC and ∠AOD form a linear pair.
So, ∠AOC + ∠AOD = 180^o
⇒ ∠AOC + 140^o = 180^o
⇒ ∠AOC = 180^o – 140^o = 40^o
Since, ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠AOC = ∠BOD
⇒ ∠BOD = 40^o
∴ ∠BOC = 140^o, ∠AOC = 40^o , ∠AOD = 140^o and ∠BOD = 40^o.

Question 12:
Since ∠COB and ∠BOD form a linear pair
So, ∠COB + ∠BOD = 180^o
⇒ ∠BOD = 180^o – ∠COB …. (1)
Also, as ∠COA and ∠AOD form a linear pair.
So, ∠COA + ∠AOD = 180^o
⇒ ∠AOD = 180^o – ∠COA
⇒ ∠AOD = 180^o – ∠COB …. (2)
[Since, OC is the bisector of ∠AOB, ∠BOC = ∠AOC]
From (1) and (2), we get,
∠AOD = ∠BOD (Proved)

Question 13:

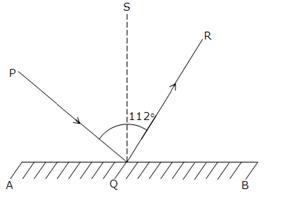
Let QS be a perpendicular to AB.
Now, ∠PQS = ∠SQR
Because angle of incident = angle of reflection
⇒ ∠PQS = ∠SQR = \(\frac { 112 }{ 2 } \) = 56^o
Since QS is perpendicular to AB, ∠PQA and ∠PQS are complementary angles.
Thus, ∠PQA + ∠PQS = 90^o
⇒ ∠PQA + 56^o = 90^o
⇒ ∠PQA = 90^o – 56^o = 34^o

Question 14:
Given : AB and CD are two lines which are intersecting at O. OE is a ray bisecting the ∠BOD. OF is a ray opposite to ray OE.

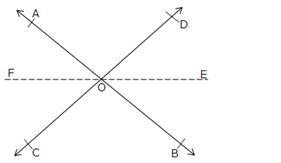
To Prove: ∠AOF = ∠COF
Proof : Since \(\overrightarrow { OE } \) and \(\overrightarrow { OF } \) are two opposite rays, \(\overrightarrow { EF } \) is a straight line passing through O.
∴ ∠AOF = ∠BOE
and ∠COF = ∠DOE
[Vertically opposite angles]
But ∠BOE = ∠DOE (Given)
∴ ∠AOF = ∠COF
Hence, proved.

Question 15:
Given: \(\overrightarrow { CF } \) is the bisector of ∠BCD and \(\overrightarrow { CE } \) is the bisector of ∠ACD.
To Prove: ∠ECF = 90^o
Proof: Since ∠ACD and ∠BCD forms a linear pair.
∠ACD + ∠BCD = 180^o

∠ACE + ∠ECD + ∠DCF + ∠FCB = 180^o
∠ECD + ∠ECD + ∠DCF + ∠DCF = 180^o
because ∠ACE = ∠ECD
and ∠DCF = ∠FCB
2(∠ECD) + 2 (∠CDF) = 180^o
2(∠ECD + ∠DCF) = 180^o
∠ECD + ∠DCF = \(\frac { 180 }{ 2 } \) = 90^o
∠ECF = 90^o (Proved)