RS Aggarwal Class 9 Math First Chapter Number System Exercise 1C Solution

EXERCISE 1C

Question 1:
Irrational number: A number which cannot be expressed either as a terminating decimal or a repeating decimal is known as irrational number. Rather irrational numbers cannot be expressed in the fraction form, \(\frac { p }{ q } \), p and q are integers and q ≠ 0

For example, 0.101001000100001 is neither a terminating nor a repeating decimal and so is an irrational number.
Also, \(\sqrt { 2 } ,\quad \sqrt { 5 } ,\quad \sqrt { 3 } ,\quad \sqrt { 6 } ,\quad \sqrt { 7 } \) etc are examples of irrational numbers.

Question 2:
(i) \(\sqrt { 4 } \)
We know that, if n is a perfect square, then \(\sqrt { n } \) is a rational number.
Here, 4 is a perfect square and hence, \(\sqrt { 4 } \) = 2 is a rational number.
So, \(\sqrt { 4 } \) is a rational number.

(ii) \(\sqrt { 196 } \)
We know that, if n is a perfect square, then \(\sqrt { n } \) is a rational number.
Here, 196 is a perfect square and hence \(\sqrt { 196 } \) is a rational number.
So, \(\sqrt { 196 } \) is rational.

(iii) \(\sqrt { 21 } \)
We know that, if n is a not a perfect square, then \(\sqrt { n } \) is an irrational number.
Here, 21 is a not a perfect square number and hence, \(\sqrt { 21 } \) is an irrational number.
So, \(\sqrt { 21 } \) is irrational.

(iv) \(\sqrt { 43 } \)
We know that, if n is a not a perfect square, then \(\sqrt { n } \) is an irrational number.
Here, 43 is not a perfect square number and hence, \(\sqrt { 43 } \) is an irrational number.
So, \(\sqrt { 43 } \) is irrational.

(v) \(3+\sqrt { 3 } \)
\(3+\sqrt { 3 } \), is the sum of a rational number 3 and \(\sqrt { 3 } \) irrational number .
Theorem: The sum of a rational number and an irrational number is an irrational number.
So by the above theorem, the sum, \(3+\sqrt { 3 } \), is an irrational number.

(vi) \(\sqrt { 7 } -2 \)
\(\sqrt { 7 } -2 \) = \(\sqrt { 7 } \) + (-2) is the sum of a rational number and an irrational number.
Theorem: The sum of a rational number and an irrational number is an irrational number.
So by the above theorem, the sum, \(\sqrt { 7 } \) + (-2) , is an irrational number.
So, \(\sqrt { 7 } -2 \) is irrational.

(vii) \(\frac { 2 }{ 3 } \sqrt { 6 } \)
\(\frac { 2 }{ 3 } \sqrt { 6 } \) = \(\frac { 2 }{ 3 } \) × \(\sqrt { 6 } \) is the product of a rational number and an irrational number .
Theorem: The product of a non-zero rational number and an irrational number is an irrational number.
Thus, by the above theorem, \(\frac { 2 }{ 3 } \) × \(\sqrt { 6 } \) is an irrational number.
So, \(\frac { 2 }{ 3 } \sqrt { 6 } \) is an irrational number.

(viii) 0.\(\bar { 6 } \)
Every rational number can be expressed either in the terminating form or in the non-terminating, recurring decimal form.
Therefore, 0.\(\bar { 6 } \) = 0.6666

Question 3:

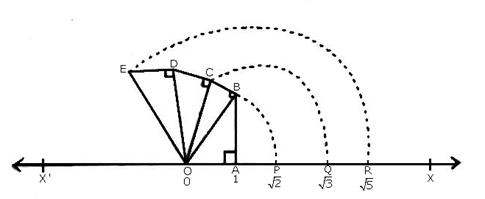
Let X’OX be a horizontal line, taken as the x-axis and let O be the origin. Let O represent 0.
Take OA = 1 unit and draw BA ⊥ OA such that AB = 1 unit, join OB. Then,

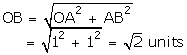
With O as centre and OB as radius, drawn an arc, meeting OX at P.
Then, OP = OB = \(\sqrt { 2 } \) units
Thus the point P represents \(\sqrt { 2 } \) on the real line.
Now draw BC ⊥ OB such that BC = 1 units
Join OC. Then,

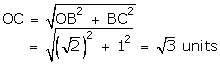
With O as centre and OC as radius, draw an arc, meeting OX at Q. The,
OQ = OC = \(\sqrt { 3 } \) units
Thus, the point Q represents \(\sqrt { 3 } \) on the real line.
Now draw CD ⊥ OC such that CD = 1 units
Join OD. Then,

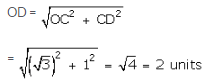
Now draw DE ⊥ OD such that DE = 1 units
Join OE. Then,

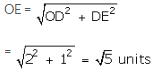
With O as centre and OE as radius draw an arc, meeting OX at R.
Then, OR = OE = \(\sqrt { 5 } \) units
Thus, the point R represents \(\sqrt { 5 } \) on the real line.

Question 4:

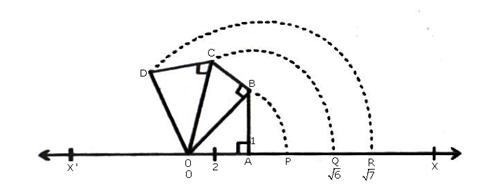
Draw horizontal line X’OX taken as the x-axis
Take O as the origin to represent 0.
Let OA = 2 units and let AB ⊥ OA such that AB = 1 units
Join OB. Then,

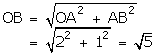
With O as centre and OB as radius draw an arc meeting OX at P.
Then, OP = OB = \(\sqrt { 5 } \)
Now draw BC ⊥ OB and set off BC = 1 unit
Join OC. Then,

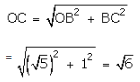
With O as centre and OC as radius, draw an arc, meeting OX at Q.
Then, OQ = OC = \(\sqrt { 6 } \)
Thus, Q represents \(\sqrt { 6 } \) on the real line.
Now, draw CD ⊥ OC as set off CD = 1 units
Join OD. Then,

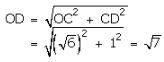
With O as centre and OD as radius, draw an arc, meeting OX at R. Then
OR = OD = \(\sqrt { 7 } \)
Thus, R represents \(\sqrt { 7 } \) on the real line.

Question 5:
(i) \(4+\sqrt { 5 } \)
Since 4 is a rational number and \(\sqrt { 5 } \) is an irrational number.
So, \(4+\sqrt { 5 } \) is irrational because sum of a rational number and irrational number is always an irrational number.

(ii) \((-3+\sqrt { 6 } ) \)
Since – 3 is a rational number and \(\sqrt { 6 } \) is irrational.
So, \((-3+\sqrt { 6 } ) \) is irrational because sum of a rational number and irrational number is always an irrational number.

(iii) \(5\sqrt { 7 } \)
Since 5 is a rational number and \(\sqrt { 7 } \) is an irrational number.
So, \(5\sqrt { 7 } \) is irrational because product of a rational number and an irrational number is always irrational.

(iv) \(-3\sqrt { 8 } \)
Since -3 is a rational number and \(\sqrt { 8 } \) is an irrational number.
So, \(-3\sqrt { 8 } \) is irrational because product of a rational number and an irrational number is always irrational.

(v) \(\frac { 2 }{ \sqrt { 5 } } \)

\(\frac { 2 }{ \sqrt { 5 } } \) is irrational because it is the product of a rational number and the irrational number \(\sqrt { 5 } \).

(vi) \(\frac { 4 }{ \sqrt { 3 } } \)

\(\frac { 4 }{ \sqrt { 3 } } \) is an irrational number because it is the product of rational number and irrational number \(\sqrt { 3 } \).

Question 6:
(i) True
(ii) False
(iii) True
(iv) False
(v) True
(vi) False
(vii) False
(viii) True
(ix) True