RS Aggarwal Class 9 Math First Chapter Number System Exercise 1B Solution

Exercise 1B

Question 1:
(i) \(\frac { 13 }{ 80 } \)

If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since, 80 has prime factors 2 and 5, \(\frac { 13 }{ 80 } \) is a terminating decimal.

(ii) \(\frac { 7 }{ 24 } \)

If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since, 24 has prime factors 2 and 3 and 3 is different from 2 and 5,
\(\frac { 7 }{ 24 } \) is not a terminating decimal.

(iii) \(\frac { 5 }{ 12 } \)

If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since 12 has prime factors 2 and 3 and 3 is different from 2 and 5,
\(\frac { 5 }{ 12 } \) is not a terminating decimal.

(iv) \(\frac { 8 }{ 35 } \)

If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since 35 has prime factors 5 and 7, and 7 is different from 2 and 5,
\(\frac { 8 }{ 35 } \) is not a terminating decimal.

(v) \(\frac { 16 }{ 125 } \)

If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since 125 has prime factor 5 only
\(\frac { 16 }{ 125 } \) is a terminating decimal.

Question 2:
(i)\(\frac { 5 }{ 8 } \)

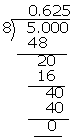
\(\frac { 5 }{ 8 } \) = 0.625

(ii) \(\frac { 9 }{ 16 } \)

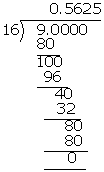
\(\frac { 9 }{ 16 } \) = 0.5625

(iii) \(\frac { 7 }{ 25 } \)

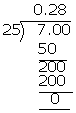
\(\frac { 7 }{ 25 } \) = 0.28

(iv)\(\frac { 11 }{ 24 } \)

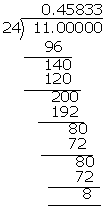
\(\frac { 11 }{ 24 } \) = 0.458\(\bar { 3 } \)

(v) \(2\frac { 5 }{ 12 } =\frac { 29 }{ 12 } \)

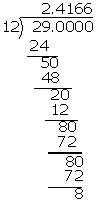
\(2\frac { 5 }{ 12 } \) = 2.41\(\bar { 6 } \)

Question 3:
(i) Let x = 0.\(\bar { 3 } \)
i.e x = 0.333 …. (i)
⇒ 10x = 3.333 …. (ii)
Subtracting (i) from (ii), we get
9x = 3
⇒ x = \(\frac { 3 }{ 9 } \) = \(\frac { 1 }{ 3 } \)
Hence, 0.\(\bar { 3 } \) = \(\frac { 1 }{ 3 } \)

(ii) Let x = 1.\(\bar { 3 } \)
i.e x = 1.333 …. (i)
⇒10x = 13.333 …. (ii)
Subtracting (i) from (ii) we get;
9x = 12
⇒ x = \(\frac { 12 }{ 9 } \) = \(\frac { 4 }{ 3 } \)
Hence, 1.\(\bar { 3 } \) = \(\frac { 4 }{ 3 } \)

(iii) Let x = 0.\(\bar { 34 } \)
i.e x = 0.3434 …. (i)
⇒ 100x = 34.3434 …. (ii)
Subtracting (i) from (ii), we get
99x = 34
⇒ x = \(\frac { 34 }{ 99 } \)
Hence, 0.\(\bar { 34 } \) = \(\frac { 33 }{ 99 } \)

(iv) Let x = 3.\(\bar { 14 } \)
i.e x = 3.1414 …. (i)
⇒ 100x = 314.1414 …. (ii)
Subtracting (i) from (ii), we get
99x = 311
⇒ x = \(\frac { 311 }{ 99 } \)
Hence, 3.\(\bar { 14 } \) = \(\frac { 311 }{ 99 } \)

(v) Let x = 0.\(\bar { 324 } \)
i.e. x = 0.324324 ….(i)
⇒ 1000x = 324.324324….(ii)
Subtracting (i) from (ii), we get
999x = 324
⇒ x = \(\frac { 324 }{ 999 } \) = \(\frac { 12 }{ 37 } \)
Hence, 0.\(\bar { 324 } \) = \(\frac { 12 }{ 37 } \)

(vi) Let x = 0.\(\bar { 17 } \)
i.e. x = 0.177 …. (i)
⇒ 10x = 1.777 …. (ii)
and 100x = 17.777…. (iii)
Subtracting (ii) from (iii), we get
90x = 16
⇒ x = \(\frac { 16 }{ 90 } \) = \(\frac { 8 }{ 45 } \)
Hence, 0.\(\bar { 17 } \) = \(\frac { 8 }{ 45 } \)

(vii) Let x = 0.\(\bar { 54 } \)
i.e. x = 0.544 …. (i)
⇒ 10 x = 5.44 …. (ii)
and 100x = 54.44 ….(iii)
Subtracting (ii) from (iii), we get
90x = 49
⇒ x = \(\frac { 49 }{ 90 } \)
Hence, 0.\(\bar { 54 } \) = \(\frac { 49 }{ 90 } \)

(vii) Let x = Let x = 0.1\(\bar { 63 } \)
i.e. x = 0.16363 …. (i)
⇒ 10x = 1.6363 …. (ii)
and 1000 x = 163.6363 …. (iii)
Subtracting (ii) from (iii), we get
990x = 162
⇒ x = \(\frac { 162 }{ 990 } \) = \(\frac { 9 }{ 55 } \)
Hence, 0.1\(\bar { 63 } \) = \(\frac { 9 }{ 55 } \)

Question 4:
(i) True. Since the collection of natural number is a sub collection of whole numbers, and every element of natural numbers is an element of whole numbers
(ii) False. Since 0 is whole number but it is not a natural number.
(iii) True. Every integer can be represented in a fraction form with denominator 1.
(iv) False. Since division of whole numbers is not closed under division, the value of \(\frac { p }{ q } \), p and q are integers and q ≠ 0, may not be a whole number.
(v) True. The prime factors of the denominator of the fraction form of terminating decimal contains 2 and/or 5, which are integers and are not equal to zero.
(vi) True. The prime factors of the denominator of the fraction form of repeating decimal contains integers, which are not equal to zero.
(vii) True. 0 can considered as a fraction \(\frac { 0 }{ 1 } \), which is a rational number.