RS Aggarwal Class 9 Math Chapter 2 Polynomials Exercise 2J Solution

EXERCISE 2J

Question 1:
x³ + 27
= x³ + 3³
= (x + 3) (x² – 3x + 9)

Question 2:
8x³ + 27y³
= (2x)³ + (3y)³
= (2x+ 3y) [(2x)² – (2x) (3y) + (3y)²]

= (2x + 3y) (4x² – 6xy + 9y²).

Question 3:
343 + 125 b³
= (7)³ + (5b)³
= (7 + 5b) [(7)² – (7) (5b) + (5b)²]

= (7 + 5b) (49 – 35b + 25b²)

Question 4:
1 + 64x³
= (1)³ + (4x)³
= (1 + 4x) [(1)² – 1 (4x) + (4x)²]

= (1 + 4x) (1 – 4x + 16x²).

Question 5:
125a³ + \(\frac { 1 }{ 8 } \)
We know that

Let us rewrite

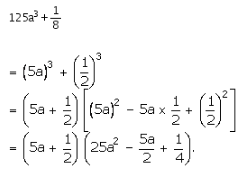
Question 6:
216x³ + \(\frac { 1 }{ 125 } \)
We know that

Let us rewrite

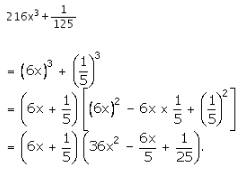
Question 7:
16x ⁴ + 54x
= 2x (8x ³ + 27)
= 2x [(2x)³ + (3)³]
= 2x (2x + 3) [(2x)² – 2x(3) + 3²]

=2x(2x+3)(4x² -6x +9)

Question 8:
7a³ + 56b³
= 7(a³ + 8b³)
= 7 [(a)³ + (2b)³]
= 7 (a + 2b) [a² – a 2b + (2b)²]

= 7 (a + 2b) (a² – 2ab + 4b²).

Question 9:
x⁵ + x²
= x²(x³ + 1)
= x² (x + 1) [(x)² – x (1) + (1)²]

= x² (x + 1) (x² – x + 1).

Question 10:
a³ + 0.008
= (a)³ + (0.2)³
= (a + 0.2) [(a)² – a(0.2) + (0.2)²]

= (a + 0.2) (a² – 0.2a + 0.04).

Question 11:
x⁶ + y⁶
= (x²)³ + (y²)³
= (x² + y²) [(x²)² – x² (y²)+ (y²)²]

= (x² + y²) (x⁴ – x²y² + y⁴).

Question 12:
2a³ + 16b³ – 5a – 10b
= 2 (a³ + 8b³) – 5 (a + 2b)
= 2 [(a)³ + (2b)³] – 5 (a + 2b)
= 2 (a + 2b) [(a)² – a (2b) + (2b)² ] – 5 (a + 2b)

= (a + 2b) [2(a² – 2ab + 4b²) – 5]

Question 13:
x³ – 512
= (x)³ – (8)³
= (x – 8) [(x)² + x (8) + (8)²]

= (x – 8) (x² + 8x + 64).

Question 14:
64x³ – 343
= (4x)³ – (7)³
= (4x – 7) [(4x)² + 4x (7) + (7)²]

= (4x – 7) (16x² + 28x + 49).

Question 15:
1 – 27x³
= (1)³ – (3x)³
= (1 – 3x) [(1)² + 1 (3x) + (3x)²]

= (1 – 3x) (1 + 3x + 9x²).

Question 16:
1 – 27x³
= (1)³ – (3x)³
= (1 – 3x) [(1)² + 1 (3x) + (3x)²]

= (1 – 3x) (1 + 3x + 9x²).

Question 17:
We know that

Let us rewrite

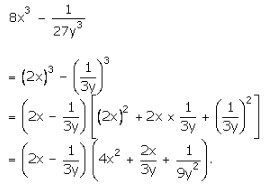
Question 18:
a³ – 0.064
= (a)³ – (0.4)³
= (a – 0.4) [(a)² + a (0.4) + (0.4)²]

= (a – 0.4) (a² + 0.4 a + 0.16).

Question 19:
(a + b)³ – 8
= (a + b)³ – (2)³
= (a + b – 2) [(a + b)² + (a + b) 2 + (2)²]

= (a + b – 2) [a² + b² + 2ab + 2 (a + b) + 4].

Question 20:
x⁶ – 729
= (x²)³ – (9)³
= (x² – 9) [(x²)² + x² 9 + (9)²]

= (x² – 9) (x⁴ + 9x² + 81)
= (x + 3) (x – 3) [(x² + 9)² – (3x)²]
= (x + 3) (x – 3) (x² + 3x + 9) (x² – 3x + 9).

Question 21:
We know that,

Therefore,
(a + b)³ – (a – b)³
= [a + b – (a – b)] [ (a + b)² + (a + b) (a – b) + (a – b)²]
= (a + b – a + b) [ a² + b² + 2ab + a² – b² + a² + b² – 2ab]
= 2b (3a² + b²).

Question 22:
x – 8xy³
= x (1 – 8y³)
= x [(1)³ – (2y)³]
= x (1 – 2y) [(1)² + 1 (2y) + (2y)²]

= x (1 – 2y) (1 + 2y + 4y²).

Question 23:
32x⁴ – 500x
= 4x (8x³ – 125)
= 4x [(2x)³ – (5)³]
= 4x [(2x – 5) [(2x)² + 2x (5) + (5)²]

= 4x (2x – 5) (4x² + 10x + 25).

Question 24:
3a⁷b – 81a⁴b⁴
= 3a⁴b (a³ – 27b³)
= 3a⁴b [(a)³ – (3b)³]
= 3a⁴b (a – 3b) [(a)² + a (3b) + (3b)²]

= 3a⁴b (a – 3b) (a² + 3ab + 9b²).

Question 25:
We know that

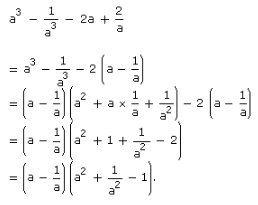
Question 26:
8a³ – b³ – 4ax + 2bx
= 8a³ – b³ – 2x (2a – b)
= (2a)³ – (b)³ – 2x (2a – b)
= (2a – b) [(2a)² + 2a (b) + (b)²] – 2x (2a – b)

= (2a – b) (4a² + 2ab + b²) – 2x (2a – b)
= (2a – b) (4a² + 2ab + b² – 2x).

Question 27:
8a³ – b³ – 4ax + 2bx
= 8a³ – b³ – 2x (2a – b)
= (2a)³ – (b)³ – 2x (2a – b)
= (2a – b) [(2a)² + 2a (b) + (b)²] – 2x (2a – b)

= (2a – b) (4a² + 2ab + b²) – 2x (2a – b)
= (2a – b) (4a² + 2ab + b² – 2x).