RS Aggarwal Class 9 Math First Chapter Number System Exercise 1D Solution

EXERCISE 1D

Question 1:
(i)

We have:

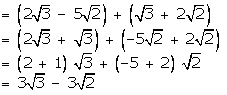
(ii)

We have:

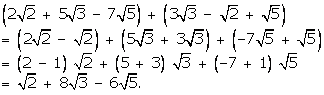
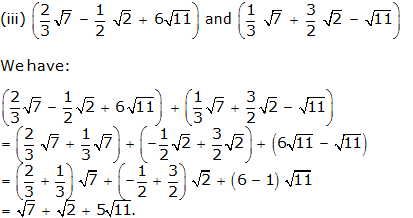
Question 2:

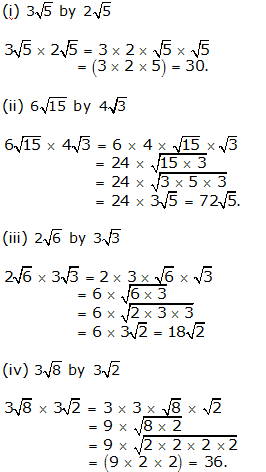
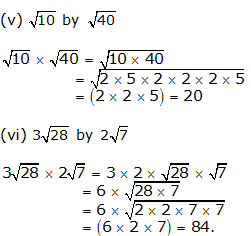
Question 3:
(i) \(16\sqrt { 6 } \) by \(4\sqrt { 2 } \)

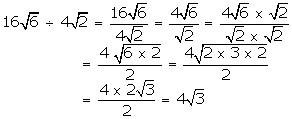
(ii) \(12\sqrt { 15 } \) by \(4\sqrt { 3 } \)

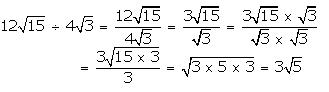
(iii) \(18\sqrt { 21 } \) by \(6\sqrt { 7 } \)

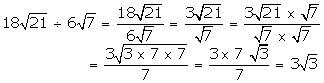
Question 4:

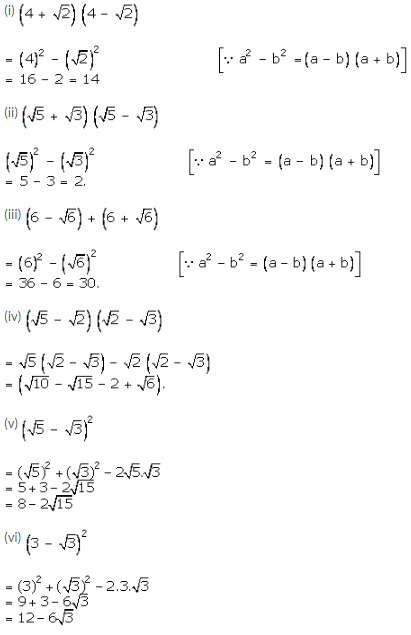
Question 5:

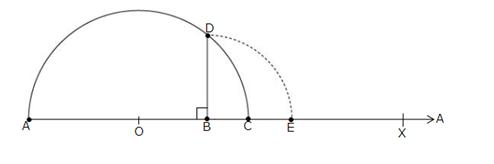
Draw a line segment AB = 3.2 units and extend it to C such that BC = 1 units.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD AC, intersecting the semicircle at D.
Then, BD = \(\sqrt { 3.2 } \) units.
With B as centre and BD as radius, draw an arc meeting AC produced at E.
Then, BE = BD = \(\sqrt { 3.2 } \) units.

Question 6:

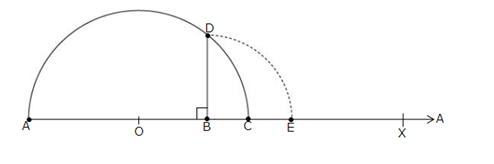
Draw a line segment AB = 7.28 units and extend it to C such that BC = 1 unit.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD AC, intersecting the semicircle at D.
Then, BD = \(\sqrt { 7.28 } \) units.
With D as centre and BD as radius, draw an arc, meeting AC produced at E.
Then, BE = BD = \(\sqrt { 7.28 } \) units.

Question 7:
Closure Property: The sum of two real numbers is always a real number.
Associative Law: (a + b) + c = a + (b + c) for al real numbers a, b, c.
Commutative Law: a + b = b + a, for all real numbers a and b.
Existence of identity: 0 is a real number such that 0 + a = a + 0, for every real number a.
Existence of inverse of addition: For each real number a, there exists a real number (-a) such that
a + (-a) = (-a) + a= 0
a and (-a) are called the additive inverse of each other.
Existence of inverse of multiplication:
For each non zero real number a, there exists a real number \(\frac { 1 }{ a } \) such that

a and \(\frac { 1 }{ a } \) are called the multiplicative inverse of each other.